Циклом называют повторение одних и тех же действий (шагов). Последовательность действий, которые повторяются в цикле, называют телом цикла. Существует несколько типов алгоритмов циклической структуры. На рис. 2.1 изображен цикл с предусловием, а на рис. 2.2 — цикл с постусловием, которые называют условными циклическими алгоритмами. Нетрудно заметить, что эти циклы взаимозаменяемы и обладают некоторыми отличиями.
- в цикле с предусловием условие проверяется до тела цикла, в цикле с постусловием — после тела цикла;
- в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с предусловием тело цикла может не выполниться ни разу;
- в цикле с предусловием проверяется условие продолжения цикла, в цикле с постусловием — условие выхода из цикла.
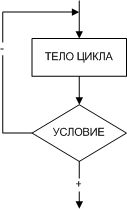 |  |
| Рис. 2.1. Алгоритм циклической структуры с предусловием | Рис. 2.2. Алгоритм циклической структуры с постусловием При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла. Кроме того, существует так называемый безусловный циклический алгоритм (рис. 2.3), который удобно использовать, если известно, сколько раз необходимо выполнить тело цикла. |
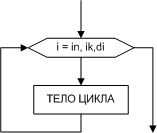 |
| Рис. 2.3. Алгоритм циклической структуры без условия |
Выполнение безусловного циклического алгоритма начинается с присвоения переменной i стартового значения in. Затем следует проверка, не превосходит ли переменная i конечное значение iк. Если превосходит, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и переменная i меняет свое значение в соответствии с указанным шагомdi. Далее, снова производится проверка значения переменной i и алгоритм повторяется. Понятно, что безусловный циклический алгоритм можно заменить любым условным. Например, так как показано на рис. 2.4.
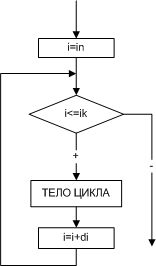 |
| Рис. 2.4. Условный циклический алгоритм с известным числом повторений |
Отметим, что переменную i называют параметром цикла, так как это переменная, которая изменяется внутри цикла по определенному закону и влияет на его окончание.
ПРИМЕР 2.1. Найти наибольший общий делитель (НОД) двух натуральных чисел А и В.
Входные данные: А и В.Выходные данные: А — НОД.
Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными, так, как показано в таблице 2.1.
| Таблица 2.1. Поиск НОД для чисел А=25 и В=15. | ||||
| Исходные данные | Первый шаг | Второй шаг | Третий шаг | НОД(А,В)=5 |
| А=25 | А=10 | А=10 | А=5 | |
| В=15 | В=15 | В=5 | В=5 |
В блок-схеме решения задачи, представленной на рис. 2.5, для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В.
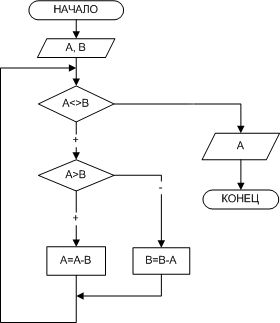 |
| Рис. 2.5. Поиск наибольшего общего делителя двух чисел |
Контрольные задания



